Pratiquant le tennis de table depuis de nombreuses années, je me suis penché sur un phénomène bien connu des pongistes et surnommé “carotte”. Il s’agit d’un point qui se termine sur un coup “hasardeux” faisant tomber la balle sous sur la bande du filet, puis du côté adverse, soit sur l’une des trois arêtes de la demi-table adverse.
Un phénomène assez étonnant semble être la sur-proportion de balles hautes (coup de défense jouée par l’opposant) tombant sur l’arête de la table comme en témoigne cette compilation de la chaîne Monqui Pong. Simple hasard ou régularité statistique ? Y a-t-il une ou plusieurs explications scientifiques à cela ?
[NDA : il y aura deux manières de lire cet article, l’une portée sur le modèle d’intelligence artificielle utilsé, l’autre sur les aspects purement liés au tennis de table. Certains lecteurs seront sans doute intéressés par les deux !]

Pour nous aider, nous allons faire appel au plus doué des modèles de langage : o1 de la société OpenAI. Ce modèle a la particularité d’avoir intégré les chaines de pensée (chain of thought) lors de son entrainement et donc de pouvoir reproduire des raisonnements complexes.
On a souvent entendu dire que les modèles de fondation ne disposaient pas d’une connaissance physique du monde et c’est pourquoi les générateurs d’images ou de vidéos pouvaient produire des aberrations physiques ou mécaniques, choquant ainsi notre perception humaine.
Rappelons-nous toutefois que nous sommes tous passés par la phase expérimentale du jet d’objets depuis notre chaise haute de bébé pour tester la gravité universelle ! C’est cette expérience continue du quotidien qui nous permet ensuite de considérer les lois physiques comme “naturelles” et si évidentes.
Déploiement du modèle o1 dans Azure
Le modèle o1 est à ce jour (janvier 2025) disponible dans les régions East US2 et Sweden Central, en mode “Global Standard”. Afin de réaliser le déploiement, il est nécessaire de remplir un formulaire de demande d’accès.
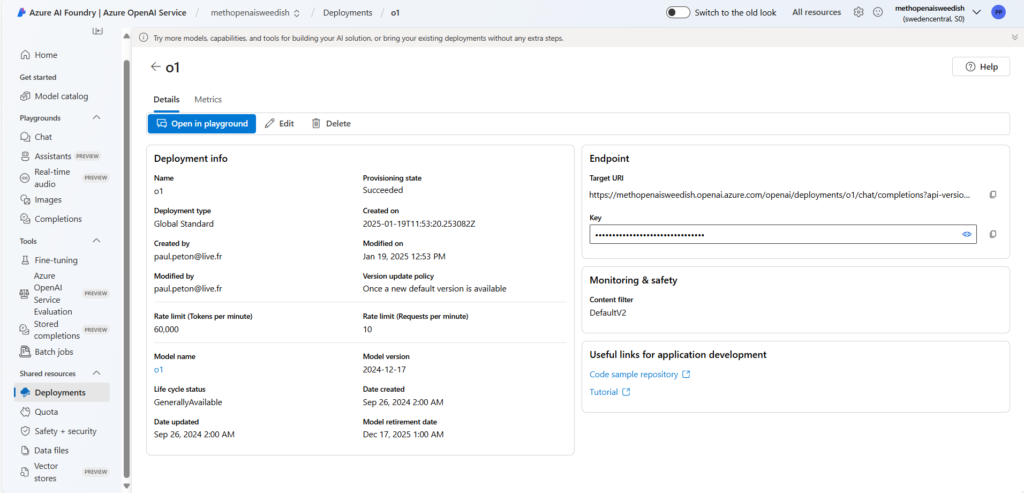
Le modèle dispose de connaissances allant jusqu’à octobre 2023, il connaît donc les dimensions officielles d’une table de ping-pong ainsi que les caractéristiques des balles plastiques.
Comparaison des réponses entre o1 et ChatGPT
Probabilité de toucher l’arête
Testons un premier prompt qui donner la probabilité de toucher l’arête de la demi-table adverse.
Soit une table de ping-pong vue de dessus, aux dimensions officielles. En posant l’hypothèse que l’arête de la table mesure 1 millimètre, quelle est la probabilité que la balle touche l’une des trois arêtes de la table adverse ? On considèrera une répartition uniforme des balles sur la table, sauf si d’autres lois mathématiques permettent de modifier cette hypothèse.
<DEBUT DE LA REPONSE DU MODELE o1>
Pour répondre à cette question, il faut d’abord préciser les dimensions officielles d’une table de ping-pong : elle mesure 2,74 m de long et 1,525 m de large. Le filet la partage en deux moitiés égales, chacune de 1,37 m × 1,525 m. Vue de dessus, « la table adverse » peut donc être modélisée par un simple rectangle de 1,37 m sur 1,525 m, dont on veut connaître la probabilité qu’un point (où la balle atterrit) se trouve à 1 mm ou moins d’une des trois arêtes extérieures (on ne compte pas le côté du filet).
Aire totale de la demi-table
L’aire A de la demi-table est A = 1,37 m × 1,525 m = 2,08825 m².
Aire « au bord » de chacune des arêtes
Les deux arêtes latérales (longueur 1,37 m) :
chacune est bordée, sur toute sa longueur, d’une bande de largeur 0,001 m (1 mm). L’aire d’une telle bande vaut donc 1,37 m × 0,001 m = 0,00137 m²
et comme il y en a deux, l’aire totale pour ces deux côtés est 2 × 0,00137 m² = 0,00274 m².
L’arête du fond (largeur 1,525 m) : elle est bordée d’une bande de même largeur (1 mm), d’aire 1,525 m × 0,001 m = 0,001525 m².
En additionnant ces aires, on obtient 0,00274 m² + 0,001525 m² = 0,004265 m². Cependant, on compte deux fois les petites zones de recouvrement dans les deux coins (là où une arête latérale et l’arête du fond se croisent). Chacune de ces zones de recouvrement est un carré de côté 1 mm = 0,001 m, donc d’aire 0,001 m × 0,001 m = 1×10⁻⁶ m². Il y a deux coins, donc une aire totale de 2 × 1×10⁻⁶ m² = 2×10⁻⁶ m² à soustraire une fois de la somme précédente.
La « surface au bord » corrigée vaut donc
S_bord = 0,004265 m² − 2×10⁻⁶ m² = 0,004263 m²
(en pratique, la différence est très faible).
Probabilité de toucher un bord
Si l’on suppose que la balle « atterrit » de façon uniforme sur la demi-table (hypothèse simplificatrice), la probabilité P de toucher l’une des trois arêtes extérieures est le rapport
P = S_bord / A
soit
P ≈ 0,004263 m² / 2,08825 m² ≈ 0,00204.
En pourcentage, cela donne environ 0,00204 × 100 % ≈ 0,20 %.
RÉPONSE
Sous l’hypothèse d’une répartition uniforme des balles et en négligeant les effets du filet, la probabilité qu’une balle touche l’une des trois arêtes extérieures de la demi-table adverse est d’environ 0,2 %.
<FIN DE LA REPONSE DU MODELE o1>
Le modèle o1 nous propose un raisonnement se décomposant en différentes étapes permettant d’arriver à une conclusion. Chacune de ces étapes comporte des calculs mathématiques dont les valeurs peuvent être reprises aux étapes suivantes. Nous sommes bien loin des premiers balbutiements du modèles GPT 3.5 avec les chiffres !
Les logs de l’appel au modèle nous renseigne sur les tokens utilisés. La facturation portera sur les tokens utilisés dans le prompt (la question), la complétion (la réponse) mais également lors des étapes de raisonnement qui ne sont pas visibles pour l’utilisateur.
“completion_tokens”: 3233,
“prompt_tokens”: 111,
“total_tokens”: 3344,
“completion_tokens_details”: {
“accepted_prediction_tokens”: 0,
“audio_tokens”: 0,
“reasoning_tokens”: 2304,
“rejected_prediction_tokens”: 0
Les tokens de raisonnement ne sont pas visibles via l’API mais ils seront en revanche bien facturés ! La société OpenAI justifie ceci dans cette documentation.
L’appel au modèle o1 peut, de temps en temps, ne pas donner de réponse en raison de la longueur de la réponse qui dépasse le paramètre par défaut (4096 tokens). Les logs seront alors comme tels.
“finish_reason”: “length”,
“index”: 0,
“logprobs”: null,
“message”: {
“content”: “”,
“refusal”: null,
“role”: “assistant”}
Les paramètres sont visibles dans l’interface Azure.

En Python, le code ci-dessous modifie la valeur maximale pour la complétion.
max_completion_tokens=8192LLa question similaire soumise à ChatGPT, dans sa version gratuite, nous donne la réponse suivante :

Nous remarquons une première erreur de raisonnement puisque ce n’est pas la demi-table de l’adversaire qui est considérée mais bien le côté complet (2,74m). Le modèle o1 a bien évité cette erreur.
Les pongistes retiendront que sur 1000 balles tombant “au hasard” sur la demi-table adverse, deux seulement devraient toucher l’arête.
Hypothèse de l’attraction des corps
Une idée (farfelue ?) déjà entendue dans une salle de ping est que l’attraction de deux corps (la table et la table) “détournerait” la balle d’une trajectoire sortante pour qu’elle vienne frôler l’arête de la table. Soumettons donc cette question à o1, à l’aide du prompt ci-dessous.
Soit une table de ping-pong vue de dessus, aux dimensions officielles. On définit comme une “carotte” l’impact de la balle sur une des tranches supérieures de la demi-table de l’adversaire. L’attraction des corps entre la balle et l’arête est-elle suffisante pour attirer une balle tombant d’une certaine hauteur et augmenter la probabilité d’une carotte ? Utilise le poids et la dimension officiels d’une balle.
<DEBUT DE LA REPONSE DU MODELE o1>
Pour répondre à cette question, il faut évaluer l’ordre de grandeur de la force d’attraction gravitationnelle entre la balle et l’arête de la table, puis comparer cette force à d’autres forces en jeu (en particulier le poids de la balle), afin de déterminer si elle est significative.
Données de base
- Masse d’une balle de tennis de table (officielle) : m_b = 2,7 g = 2,7×10⁻³ kg
- Diamètre d’une balle : environ 40 mm
- Masse typique d’une demi-table (en considérant le cadre + panneau) : on peut estimer une cinquantaine de kg pour simplifier (m_t = 50 kg), même si cela peut varier.
- Constante de gravitation universelle : G ≈ 6,67×10⁻¹¹ N·m²·kg⁻²
- Accélération de la pesanteur : g ≈ 9,81 m·s⁻²
Le poids de la balle, c’est-à-dire la force qui l’attire vers le sol, vaut :
F_poids = m_b × g = 2,7×10⁻³ × 9,81 ≈ 2,65×10⁻² N
Force gravitationnelle entre la balle et l’arête
Si l’on modélise (de façon très grossière) la portion de table à proximité de l’arête comme un « bloc » de masse m_t, et que la distance entre le centre de la balle et le bloc soit de l’ordre du centimètre (r = 0,01 m), la force gravitationnelle F_g entre la balle et la table se calcule par la loi de Newton :
F_g = G × (m_b × m_t) / r²
Substituons les valeurs (en prenant m_t = 50 kg, r = 0,01 m) :
F_g = 6,67×10⁻¹¹ × (2,7×10⁻³ × 50) / (0,01)²
= 6,67×10⁻¹¹ × (1,35×10⁻¹) / 10⁻⁴
= 6,67×10⁻¹¹ × 1,35×10⁻¹ × 10⁴
= 6,67×10⁻¹¹ × 1,35×10⁻¹ × 10⁴
Faisons l’estimation pas à pas :
1,35×10⁻¹ = 0,135
6,67×10⁻¹¹ × 0,135 ≈ 9×10⁻¹² (en arrondissant)
Multiplié par 10⁴ donne à peu près 9×10⁻⁸ N
Autrement dit : F_g ≈ 9×10⁻⁸ N
Comparaison à d’autres forces
Le poids de la balle est d’environ 2,65×10⁻² N.
La force gravitationnelle due à l’arête de la table : ≈ 9×10⁻⁸ N.
On constate que F_g est plus d’un million de fois plus faible que le poids de la balle (un rapport d’environ 10⁻⁶). Même en tenant compte d’approximations (distance un peu plus courte, table un peu plus massive, etc.), il est clair que cette force d’attraction est négligeable : elle ne peut pas « attirer » la balle de manière significative pour favoriser un rebond sur l’arête.
Conclusion
L’attraction gravitationnelle entre la balle de ping-pong et l’arête de la table est extrêmement faible comparée au poids de la balle et aux autres forces (rebond, frottements de l’air, etc.). Elle n’influence donc pratiquement pas la trajectoire. Autrement dit, non, cette attraction ne peut pas augmenter la probabilité de réaliser une « carotte » (rebond sur l’arête supérieure).
En pratique, le fait qu’une balle tombe sur l’arête résulte surtout de la trajectoire initiale, de la vitesse, de l’effet (spin) éventuel, et bien sûr d’un peu de hasard — mais pas d’une quelconque « force d’attraction » exercée par l’arête de la table.
<FIN DE LA REPONSE DU MODELE o1>
Les pongistes ne retiendront donc pas cette hypothèse d’attraction entre la table et la balle.
[NDA : ici s’arrête l’article pour les personnes qui ne s’intéressent qu’à l’intelligence artificielle. Les pongistes peuvent continuer.]
Augmenter la probabilité d’une carotte ?
Au gré des échanges avec ChatGPT, j’ai soumis le prompt suivant, lui laissant libre cours pour proposer ses solutions.
Soit une table de ping-pong vue de dessus, aux dimensions officielles. On définit comme une ‘carotte’ l’impact de la balle sur une des arêtes supérieures de la demi-table de l’adversaire ou bien le fait d’accrocher le filet et de retomber sur la demi-table adverse. Propose-moi une ou plusieurs approches basées sur les lois de la physique pour augmenter la probabilité d’une carotte.
Une proposition attire mon attention.

Cette excellente vidéo disponible sur la chaîne ARTE vous apprendra tout sur l’effet Magnus.
Mais y aurait-il un impact d’une hauteur initiale plus grande sur la trajectoire de la balle l’amenant à toucher le bord de table ? La question mérite d’être étudiée mais on peut la reformuler différemment. En effet, il est quasi impossible pour l’adversaire de remettre une balle qui toucherait l’arête mais n’aura pas un rebond “vers le haut”. La balle effleure l’arête et prolonge alors sa course vers le sol. Le prompt suivant formule cette question.
Soit une table de ping-pong vue de dessus, aux dimensions officielles. On définit comme une ‘carotte’ l’impact de la balle sur une des arêtes supérieures de la demi-table de l’adversaire ou bien le fait d’accrocher le filet et de retomber sur la demi-table adverse. Etablis une démonstration scientifique pour identifier les caractéristiques nécessaires à la balle (vitesse, hauteur, rotation, surface de contact avec la table…) pour ne pas rebondir vers le haut lorsqu’elle tombe sur l’arête de la demi-table adverse.
<DEBUT DE LA REPONSE DU MODELE o1>
D’un point de vue purement physique, l’« effet carotte » (c’est‐à‐dire le fait qu’une balle de ping‐pong percute l’arête supérieure de la demi‐table adverse et « glisse » au lieu de rebondir vers le haut) peut s’analyser comme un choc avec un obstacle situé au bord de la table, combiné à des effets de frottement et de rotation. L’objectif est de déterminer les conditions (vitesse, hauteur, rotation, etc.) pour que la composante verticale finale de la vitesse de la balle (dans le repère de la table) soit nulle ou dirigée vers le bas, de sorte que la balle ne « saute » pas mais « file » au ras de la table.
Modélisation du système
Repères et hypothèses simplificatrices
On se place dans un repère où le plan de la table coïncide avec le plan (x,y), et l’axe z est vertical (z>0 vers le haut).
L’arête supérieure (ou le bord) de la demi‐table adverse est schématiquement modélisée comme un « coin » horizontal dont l’arête est à z=0.
La balle (de rayon R) entre en contact avec l’arête à un instant t₀, avec une vitesse (vectorielle) du centre de gravité V = (Vₓ, Vᵧ, V𝓏) et une rotation ω = (ωₓ, ωᵧ, ω𝓏).
On suppose un choc partiellement inélastique caractérisé par un coefficient de restitution e < 1 dans la direction normale au plan de contact, et l’existence d’une force de frottement (coefficient µ) dans la direction tangentielle.
Contact et normal de choc
Au moment du contact, la normale de choc n → est (en première approche) dirigée horizontalement ou légèrement vers le haut/vers le bas selon la géométrie réelle de l’arête (on peut l’assimiler à une surface verticale ou oblique).
Toutefois, on retiendra l’idée générale : il y a toujours une décomposition de la vitesse relative de la balle au point de contact entre :
– Composante normale Vₙ = V · n → (scalaire)
– Composante tangentielle Vₜ = V − (Vₙ n →)
Décomposition du choc et conditions de rebond
Coefficient de restitution (choc normal)
Le changement de la composante normale de la vitesse s’écrit, dans le cas d’un choc central simple avec coefficient de restitution e :
Vₙ′ = − e Vₙ
où Vₙ est la composante normale de la vitesse juste avant l’impact, et Vₙ′ celle juste après.
Si e < 1, la vitesse normale est réduite en amplitude et inversée de sens (rebond « inélastique »).
Dans l’idéal (e=0), la balle « s’écrase » complètement dans la direction normale et ne repart pas (aucune composante normale après le choc).
Frottement et transfert de rotation
Le point de contact subit également une force tangentielle de frottement Fₒₜ. Dans le cas d’une balle en rotation, l’effet du frottement peut être décomposé en :
- Une force tangentielle (au point de contact) qui modifie la composante tangentielle de la vitesse du centre de gravité.
- Un couple de frottement qui agit sur la balle et modifie sa rotation.
Suivant le signe de ω et la direction de la vitesse tangentielle, la balle peut :
- Accélérer (ou décélérer) dans la direction tangentielle,
- Augmenter (ou diminuer) sa rotation.
Le frottement peut donc contribuer à « plaquer » la balle vers le bas si la rotation et la direction du frottement s’y prêtent (par exemple, balle avec un backspin approprié).
Condition pour « ne pas repartir vers le haut »
On souhaite que la composante verticale finale V𝓏′ de la balle (après la
collision) soit ≤ 0. Or, V𝓏′ résulte :
De la restitution dans la direction normale (si la normale de contact a une composante verticale),
Des effets du frottement (la force tangentielle peut avoir une composante verticale si la géométrie de l’arête l’impose, ou si la balle « mord » légèrement le haut de la table),
De la modification de la rotation qui peut influer sur la direction de glissement. En schématisant la direction normale au choc comme ayant un angle α par rapport à l’horizontale (α = 0 si la surface de contact est parfaitement verticale), la composante verticale de la vitesse normale finale devient :
V𝓏′(normal) =(− e |Vₙ|) sin α ,
alors que la composante tangentielle (considérant un frottement µ et un bras de levier R pour la balle) peut générer une correction ∆V𝓏′(tan
gent) dépendant du couple et de la vitesse tangentielle initiale. Au premier ordre, on écrit souvent :
|∆V𝓏′(tangent)| ≈ f ( µ, Vₜ, ω, R )
La condition pour que le résultat global soit V𝓏′ = V𝓏′(normal) + ∆V𝓏′(tangent) ≤ 0 nous donne l’inégalité à satisfaire :
(− e |Vₙ|) sin α + f(µ, Vₜ, ω, R) ≤ 0
Le terme f(µ, Vₜ, ω, R) peut être soit positif, soit négatif, selon le sens du frottement et l’effet de la rotation (backspin, topspin, etc.).
Analyse qualitative des paramètres requis
Pour qu’il n’y ait pas de rebond vers le haut, plusieurs conditions pratiques se dégagent :
Composante verticale initiale (avant choc) faible ou négative :
– Si la balle arrive presque horizontalement (V𝓏 < 0, c’est‐à‐dire légèrement en descente), le choc peut la contraindre à poursuivre vers le bas ou à rester rasante.
– Si la balle a une composante verticale trop grande vers le bas, elle risque d’impacter fortement l’arête et rebondir (même si c’est un rebond faible, il peut y avoir un « saut » vers le haut).
Vitesse horizontale élevée et angle rasant :
– Une forte vitesse horizontale (Vₓ ou Vᵧ) diminue le temps de contact et réduit l’élévation éventuelle post‐choc.
– Plus l’angle d’incidence est rasant (de faible α par rapport à la table), plus la balle est « glissante » au contact, ce qui favorise l’effet « carotte ».
Rotation adaptée :
– Un backspin (rotation « rétro ») approprié crée une composante tangentielle au contact qui, couplée au frottement, peut appliquer à la balle un effort dirigé vers le bas.
– Un topspin (rotation « avant ») a tendance au contraire à faire remonter la balle après contact si la friction agit dans le sens de faire rouler la balle sur la table.
Coefficient de restitution et frottement :
– Un matériau de la balle et/ou de la table avec un coefficient de restitution faible (e petit) limite l’énergie renvoyée à la balle dans la direction normale : le rebond est donc plus « amorti ».
– Un coefficient de frottement suffisant (µ) peut consolider l’effet d’adhérence, permettant de convertir une partie de la vitesse tangentielle en couple et de tirer la balle vers le bas si la rotation le permet.
Conclusion pratique
Pour qu’une balle de ping‐pong ne rebondisse pas vers le haut en touchant précisément l’arête supérieure de la demi‐table adverse (et qu’elle « glisse » ou « tombe » sur la table au lieu de « sauter »), il faut réunir :
- Une incidence suffisamment rasante (faible hauteur de chute ou vitesse essentiellement horizontale).
- Un coefficient de restitution globalement faible dans la direction du choc (e petit dans la mesure du possible).
- Une rotation (typiquement un backspin ou une rotation « latérale adéquate ») qui, par le frottement, aide à orienter la résultante du choc vers le bas ou à annuler la composante verticale finale.
- Une vitesse verticale descendante minimale (ou nulle) juste avant l’impact pour éviter un choc normal trop fort qui renverrait la balle vers le haut.
En pratique, cela se traduit souvent par un geste très précis : la balle frôle littéralement l’arête, arrive avec un léger effet rétro ou latéral, et voit son énergie de rebond absorbée par la combinaison du choc inélastique et du glissement/frottement sur l’arête ou le filet. Ainsi, elle ne « saute » pas mais poursuit sa course rase sur la demi‐table adverse, réalisant alors la fameuse « carotte ».
<FIN DE LA REPONSE DU MODELE o1>
Voici les tokens qui auront été nécessaires pour développer cette démonstration :
“completion_tokens”: 4014,
“prompt_tokens”: 143,
“total_tokens”: 4157,
“completion_tokens_details”: {
“accepted_prediction_tokens”: 0,
“audio_tokens”: 0,
“reasoning_tokens”: 1920,
“rejected_prediction_tokens”: 0
A vous maintenant de jouer pour décortiquer cette réponse ou bien de retourner jouer… à la table ! Et surtout, n’oubliez pas de vous excuser après une “carotte”.
